Mandelbrot Set Viewer in Perl and Fortran

Revision 1.0 2022-08-29

Fortran and Perl are both venerable languages which have seen a lot of use over the past decades, and which continue to be developed. It is possible for Perl to call into code written in Fortran using the FFI::Platypus Perl module. We decided to test this functionality with a quick project, to wrap a Perl/Tk interface around a Fortran Mandelbrot Set routine.

Implementation

The Fortran code was adapted from the Mandelbrot Set routine available here and is mostly unchanged (code below). It requires some source files from the fortran-utils package.

The Perl code below uses a few modules, Tkx for the GUI front-end and Imager for image processing being the main ones. As the Fortran routine returns greyscale (single colour channel) data between 0 and 255, colour maps are used to better visualise the data (various colour maps in CSV form were found here). Of course it should be possible to implement the application using the PDL but that would defeat the object of the exercise.

The implementation was very straightforward, but there were a couple of intricacies when writing this code. The slowest part of the program appears not to be generating the fractal, but synchronising the data between Imager and the Tkphoto used to display the fractal in the front-end. The recipe (thanks to this code) appears to be to save the Imager data in memory as a PNG, then encode it base-64 and send it to the Tkphoto in that way.

Sharing memory between Perl and Fortran was another minor issue. At the Perl end, an array has to be declared and initalised with the correct number of entries for Fortran to fill in. In addition, the fractal on the Fortran end is manipulated as a 2D matrix, but on the Perl end is just a flat list. Since the dimensionality is known this is not an issue in this case.

Screenshots

Some screenshots of the app working are below.

Conclusions and Further Work

It is unlikely that the world requires yet another Mandelbrot Set viewer, so we are probably not going to develop this any further. In terms of the exercise, to try to link Perl and Fortran, it was a success. It could be an interesting future project to try to access larger Fortran libraries for the purpose of controlling their input and visualising their output. It could also be interesting to try to interface with Perl PDL.

Currently the only feature we would like to implement here is the ability to click and drag a zoom region on the fractal image. When we have the opportunity to do that we will update the code here.

Source Code - Fortran

! Have compiled with: gfortran -shared -fPIC -O3 -march=native -ffast-math -funroll-loops -o libmandelbrot.so types.f90 constants.f90 utils.f90 mesh.f90 do_mandelbrot.f90
! Adapted from the Fortran code at: https://www.fortran90.org/src/rosetta.html#mandelbrot-set
! Needs types.f90, constants.f90, utils.f90 and mesh.f90 from https://github.com/certik/fortran-utils
! Believe this is MIT licence

subroutine do_mandelbrot(x_min, x_max, y_min, y_max, density, fractal)

	use types, only: dp
	use constants, only: i_
	use mesh, only: linspace, meshgrid

	implicit none

	real(dp), intent(in) :: x_min, x_max, y_min, y_max
	integer, intent(in) :: density
	integer, intent(out), dimension(density, density) :: fractal

	real(dp), dimension(density, density) :: x, y, fractal_r
	complex(dp), dimension(density, density) :: c, z

	integer, parameter :: iter = 100
	integer :: n
	real(dp) :: maxv, minv

	call meshgrid(linspace(x_min, x_max, density), linspace(y_min, y_max, density), x, y)

	c = x + i_*y
	z = c
	fractal = 255

	do n = 1, iter
		where (abs(z) <= 10) z = z**2 + c
		where (fractal == 255 .and. abs(z) > 10) fractal = 254 * (n-1) / iter
	end do

	fractal = transpose(fractal)	! adjust for different row/column order between Perl and Fortran

	fractal_r = log(real(fractal, dp))

	! rescale between 0 and 255 for colour map on the Perl end
	minv = minval(fractal_r)
	fractal_r = fractal_r - minv

	maxv = maxval(fractal_r)

	if ( maxv > 0 ) then
		fractal = INT(255.0 * fractal_r / maxv)
	else
		fractal = 0
	end if

end subroutine do_mandelbrot

				

Source Code - Perl

#!/usr/bin/perl
# Mandelbrot Set Explorer v0.1

use v5.16;

use Tkx;
use Imager;
use Text::CSV;
use MIME::Base64;
use FFI::Platypus 1.00;

# connect to Fortran function which generates Mandelbrot
# Fortran Mandelbrot code adapted from https://www.fortran90.org/src/rosetta.html#mandelbrot-set
my $ffi = FFI::Platypus->new( api => 1 );
$ffi->lang("Fortran");
$ffi->lib("./libmandelbrot.so");  
$ffi->attach( do_mandelbrot => ['real_8*', 'real_8*', 'real_8*', 'real_8*', 'integer*', 'integer[]'] => 'void' );

# read in various colour maps from CSV files
my $colour_tables = read_colour_tables();

# initialise values
my $c_map = "plasma";
my $density = 700;
my ($x_min, $x_max, $y_min, $y_max) = (-2.68, 1.32, -1.5, 1.5);
my $size = $density * $density;
my @fractal = (0) x $size;		# allocate memory for the fractal, Fortran will fill it in
my $img = Imager->new(xsize => $density, ysize => $density, channels => 3);   
my $imgcount = 1; # for now give each saved png a number, see "save" button below

# initialise Mandelbrot and images
do_mandelbrot(\$x_min, \$x_max, \$y_min, \$y_max, \$density, \@fractal);	# Fortran subroutine uses pass-by-reference
mandelbrot_to_imager();

# create Tk interface with Tkx (https://tkdocs.com)
my $mw = Tkx::widget->new(".");
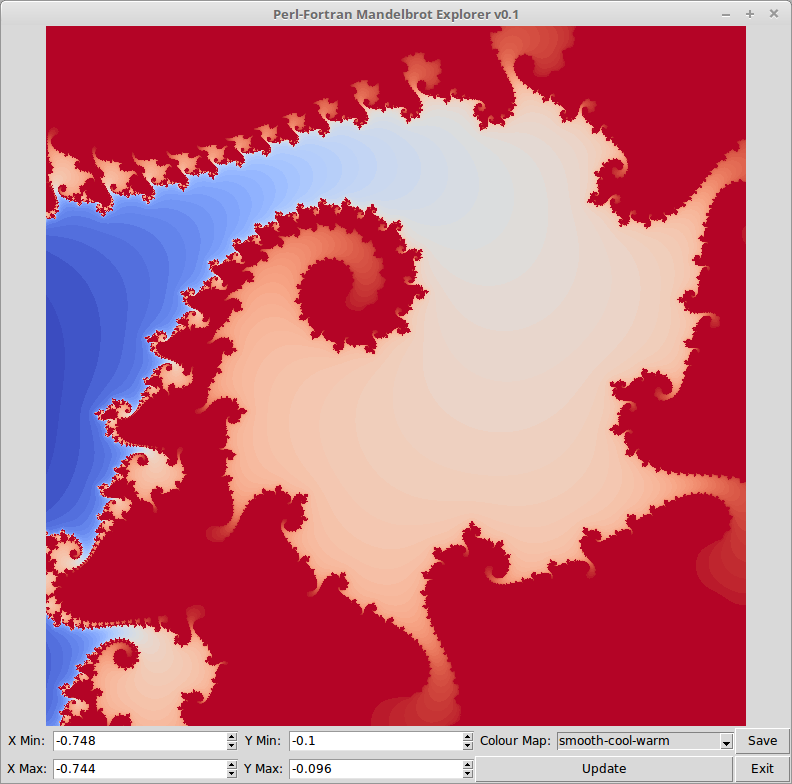
$mw->g_wm_title("Perl-Fortran Mandelbrot Explorer v0.1");
$mw->g_wm_minsize(700, 700);
my $content = $mw->new_ttk__frame;

# Tkphoto to display the fractal
my $photo_label = $content->new_ttk__label(-image => imager_to_Tkphoto());

# button to update the fractal by calling Fortran and updating the Tkphoto (via Imager)
my $update_button = $content->new_button(
	-text => "Update",
	-command => sub {	
						do_mandelbrot(\$x_min, \$x_max, \$y_min, \$y_max, \$density, \@fractal);
						mandelbrot_to_imager();						
						$photo_label->configure(-image => imager_to_Tkphoto());
						},
);

# button to save current fractal to a png file using Imager
my $save_button = $content->new_button(
	-text => "Save",
	-command => sub {
						$img->write(file => "mandelbrot_$imgcount.png");
						$imgcount++;
						},
);

# button to exit
my $exit_button = $content->new_button(
    -text => "Exit",
    -command => sub { $mw->g_destroy; },
);

# entries for x/y min/max
my $x_min_label = $content->new_ttk__label(-text => "X Min:", -padding => "5");
my $x_min_spin = $content->new_ttk__spinbox(-from => -3.0, -to => 3.0, -increment => 0.001, -textvariable => \$x_min, -format => '%.4f');

my $x_max_label = $content->new_ttk__label(-text => "X Max:", -padding => "5");
my $x_max_spin = $content->new_ttk__spinbox(-from => -3.0, -to => 3.0, -increment => 0.001, -textvariable => \$x_max, -format => '%.4f');

my $y_min_label = $content->new_ttk__label(-text => "Y Min:", -padding => "5");
my $y_min_spin = $content->new_ttk__spinbox(-from => -3.0, -to => 3.0, -increment => 0.001, -textvariable => \$y_min, -format => '%.4f');

my $y_max_label = $content->new_ttk__label(-text => "Y Max:", -padding => "5");
my $y_max_spin = $content->new_ttk__spinbox(-from => -3.0, -to => 3.0, -increment => 0.001, -textvariable => \$y_max, -format => '%.4f');

# colour map selection
my $c_map_label = $content->new_ttk__label(-text => "Colour Map:", -padding => "5");
my $c_map_combo = $content->new_ttk__combobox(-values => join(" ", keys %{$colour_tables}), -textvariable => \$c_map);
$c_map_combo->state("readonly");
$c_map_combo->g_bind(	"<<ComboboxSelected>>", 	# a new colour map selected
						sub { 
							$c_map_combo->selection_clear(); # for aesthetics, as suggested at https://tkdocs.com/tutorial/widgets.html#combobox
							mandelbrot_to_imager();	# can update colour map without going back to Fortran to recalc the fractal
							$photo_label->configure(-image => imager_to_Tkphoto());
						}); 

# create a grid to arrange all the widgets
$content->g_grid(-column => 0, -row => 0);

$photo_label->g_grid(-column => 0, -row => 0, -columnspan => 7 );

$update_button->g_grid(-column => 4, -row => 2, -columnspan => 2, -sticky => "nsew");
$save_button->g_grid(-column => 6, -row => 1, -sticky => "nsew");
$exit_button->g_grid(-column => 6, -row => 2, -sticky => "nsew");

$x_min_label->g_grid(-column => 0, -row => 1);
$x_min_spin->g_grid(-column => 1, -row => 1);

$x_max_label->g_grid(-column => 0, -row => 2);
$x_max_spin->g_grid(-column => 1, -row => 2);

$y_min_label->g_grid(-column => 2, -row => 1);
$y_min_spin->g_grid(-column => 3, -row => 1);

$y_max_label->g_grid(-column => 2, -row => 2);
$y_max_spin->g_grid(-column => 3, -row => 2);

$c_map_label->g_grid(-column => 4, -row => 1);
$c_map_combo->g_grid(-column => 5, -row => 1);

Tkx::MainLoop;

exit;

# read the colour tables from CSV files
# The colour map CSVs were found at: https://www.kennethmoreland.com/color-advice/
sub read_colour_tables {

	my $csv = Text::CSV->new ( { binary => 1 } );

	my %ct;
	my @tables = qw(
		bent-cool-warm-table-byte-0256.csv
		black-body-table-byte-0256.csv
		extended-kindlmann-table-byte-0256.csv
		inferno-table-byte-0256.csv
		kindlmann-table-byte-0256.csv
		plasma-table-byte-0256.csv
		smooth-cool-warm-table-byte-0256.csv
		viridis-table-byte-0256.csv
	);	

	foreach my $table (@tables) {

		next unless -e $table;

		open(my $fh, "<:encoding(utf8)", $table) or warn "Cannot open $table: $!";
		next unless defined $fh;

		my $table_name = substr( $table, 0, -1 * length("-table-byte-0256.csv") );

		READ_CSV: while ( my $r = $csv->getline( $fh ) ) {
			next READ_CSV unless $r->[1] =~ /\A \d+ \z/ismx;
			push @{ $ct{$table_name} }, [ $r->[1], $r->[2], $r->[3] ];
		}

		close($fh);
	}

	return \%ct;
}

# read the fractal data into Imager image via a colourmap
sub mandelbrot_to_imager {

	my @ct_to_use = @{ $colour_tables->{$c_map} };

	$img->read( type 				=> 	'raw', 
				data 				=> 	pack("C*", map { @{$ct_to_use[$_]} } @fractal ), 
				xsize 				=> 	$density, 
				ysize 				=> 	$density,
				raw_datachannels 	=> 	3, 
				raw_storechannels 	=> 	3, 
				raw_interleave 		=> 	0 
				) or die "Cannot read fractal: ", $img->errstr;
}

# push the Imager image into the Tkphoto
# method a bit involved, done as per recipe in https://metacpan.org/dist/Imager/source/samples/tk-photo.pl
sub imager_to_Tkphoto {
	
	my $image_data;

	$img->write( data => \$image_data, type => 'png' );

	$image_data = encode_base64($image_data);

	my $im = Tkx::image_create_photo( "Mandelbrot", -data => $image_data);

	return $im;
}