Inverse Model for Robot Navigation using A* Search Algorithm with Forward Models
Revision 1.0 2022-08-01
Our mobile robot base "BERTRAND" is to operate in an enclosed environment where it will have to navigate around known obstacles. A traditional approach would be to use a path-finding algorithm, such as A*, to determine a route based on a grid layout, and then a motor program would compute the motor commands for the robot to follow that route. For a robot such as Bertrand, which can rotate and move forward, this would involve hitting a succession of waypoints along the route through a sequence of alternating rotate-to-face and translate-forward motor programs.
In this brief report we explore the feasibility of a combined approach. Instead of exploring a spatial grid, we use the A* algorithm to explore the motor space of the robot, performing node traversal through simulation of possible robot commands on a forward model of the robot. The result is not a route of successive (X,Y) co-ordinates to use as a route for motor planning, but a direct computation of the sequence of motor commands that achieve the required robot navigation. In this way, the A* algorithm becomes the core of an inverse model for robot navigation.
The most obvious pitfall with this approach is the necessary discretization of the state and motor command spaces to permit graph traversal. For example, a location in metres can be described to several decimal places. The more decimal places that are used, the more accurate the trajectory, but also the larger the number of nodes to be considered by the graph search, and the longer the time it will take to calculate a path.
A related consideration is that of the branching factor. For movement, Bertrand only has two motor command parameters, one related to rotational velocity (turning) and another related to translation velocity (moving forward and back). Each of these two motor parameters can be set to a variety of values relating to greater or lesser speed. To use all of the possible motor values as parameters to create neighbouring nodes for the graph search would result in large numbers of nodes being created at each iteration of the algorithm. Thus some subset or sampling of the motor commands will probably have to take place to make the algorithm practical.
Therefore although this approach is not especially novel, it does offer challenges and advantages, and thus we explore it for our use case.
Background
Internal Models
Here we make use of the conceptual framework of internal models. In particular, our experiment aim is to created an inverse model which can produce a motor plan to move the robot from one location to another. For example. a simple move-to-location inverse model for Bertrand would consist of code to generate motor commands to rotate the robot to face the destination, followed by code to generate motor commands to move it straight forward until the destination is reached. However, that does not take into account intervening obstacles or even that the movement itself is suboptimal as the robot could be rotating and translating simultaneously. Here we anticipate that the approach will make the trajectory smoother, and enable the robot to move around obstacles to reach the goal.
More background on internal models
A* Search
A* search is described in numerous online articles. In this brief report the inverse model will make use of A* search using a forward model for traversing nodes. Essentially the inverse model will use the A* algorithm to compare and select candidate trajectories, the trajectories calculated by simulating possible motor commands on the forward model.
Implementation
Source code for experiments was written in C++ (see below for code example). SFML was used for graphic display of the computed trajectories.
State and Motor Representation
It is possible for state space representations to become complicated in code, however here we use a flat array of five double values to represent the state of the robot as it navigates: the X, Y, Θ (orientation angle of the robot), ΔΘ (angular velocity) Δp (translational velocity). Displacements are measured in metres and angles in degrees. The forward model uses all the states, and the A* search uses only the X,Y positions. Although X,Y locations are potentially continuous variables, the A* requires discrete nodes for its graph traversal formulation, and so it was decided that it would operate on a 1 cm2 representation. In an environment of 10 m2. the algorithm then has a potential to consider 1 million nodes.
For movement of its mobile base, Bertrand only has two motor command channels, one to rotate the robot and one to move it forward or backward. These command parameters effectively set motor voltages, but in this simple implementation we have them going directly to angular velocity and translational velocity. In practice, a mapping/look-up table would be required in the forward model to map the raw motor command inputs to velocities.
Robot Forward Model
The forward model for the robot is straightforwardly implemented as an Euler integrator, proceeding in the following steps:-
- The rotational velocity ΔΘ and the translational velocity Δp are determined from the passed motor command
- The angle Θ is updated from the rotational velocity ΔΘ
- The forward vector is decomposed from the angle Θ using trigonometry
- The robot X,Y position is updated from the forward vector multiplied by the translational velocity Δp
This forward model is of course very basic and gives idealised robot movement. In practice small variations in, for example, the shape of the wheels would throw this off. The forward model would then have to be calibrated with compensating constants to provide greater accuracy in prediction. It might even have to consult an environmental model for appropriate compensating constants if transitioning between for example carpeted and non-carpeted floor.
Obstacles and Collision Detection
A* is known for its ability to find paths that avoid obstacles, and this would have to be a necessary feature of this implementation, even if just a proof-of-concept. To this end, a simple collision detection was implemented using axes-aligned bounding boxes. The robot base was represented as a 20cm square box, and obstacles specified as rectangles of various sizes were used in the experiments. Nodes that were expanded into obstacle areas are simply discarded and not placed onto the A* algorithm's "open list".
Experiments and Results
Numerous experiments were run to evaluate the functioning of the approach. The images below demonstrate some of the trajectories produced, with and without obstacles. The red circle represents the starting location, the blue circle the target location, and the red line the computed trajectory. Obstacles are displayed in purple. The scale is 1 pixel to 1 cm2 (note that the green grid lines are at every 50cm and are not the grid the A* algorithm is using. A node in the A* search is 1 pixel in dimension in these images).
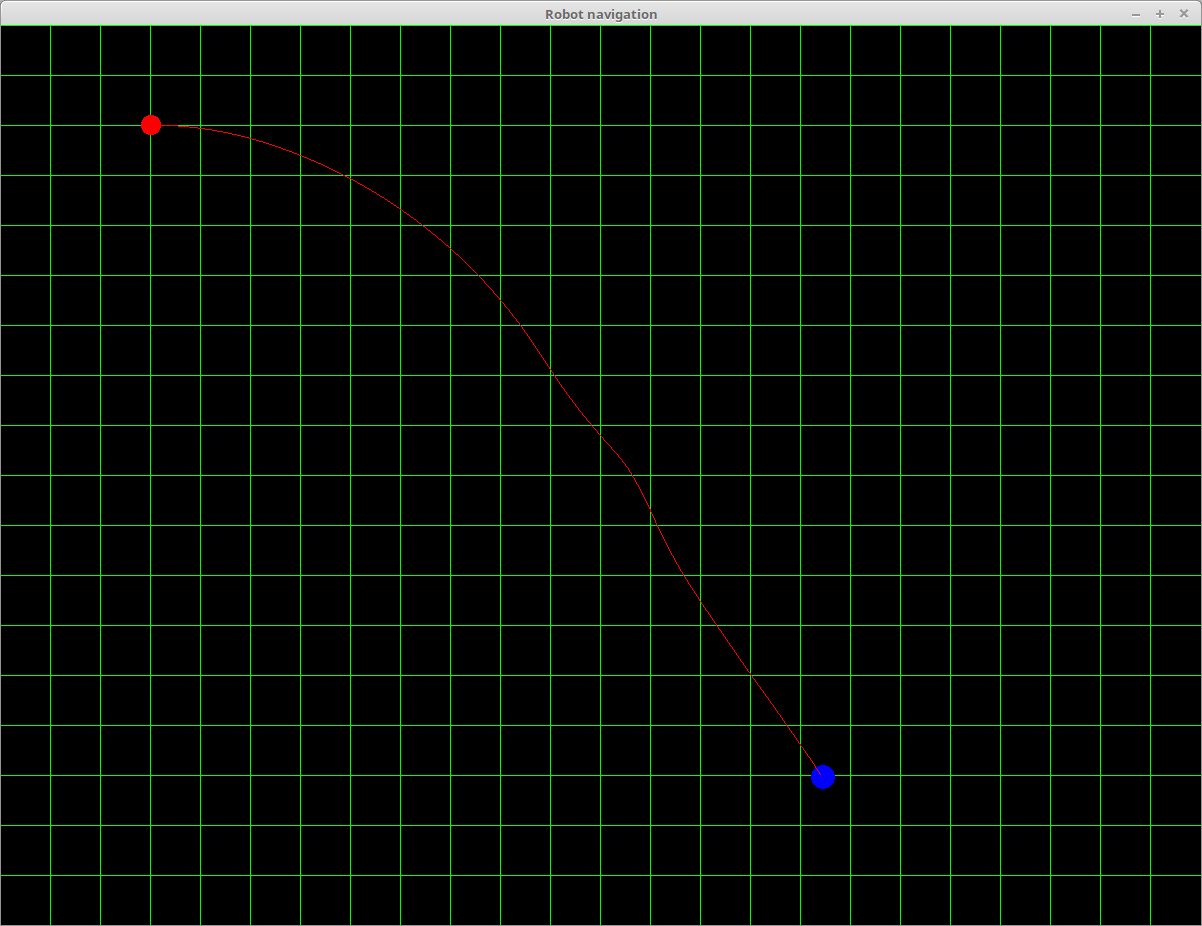
A trajectory with no obstacles.
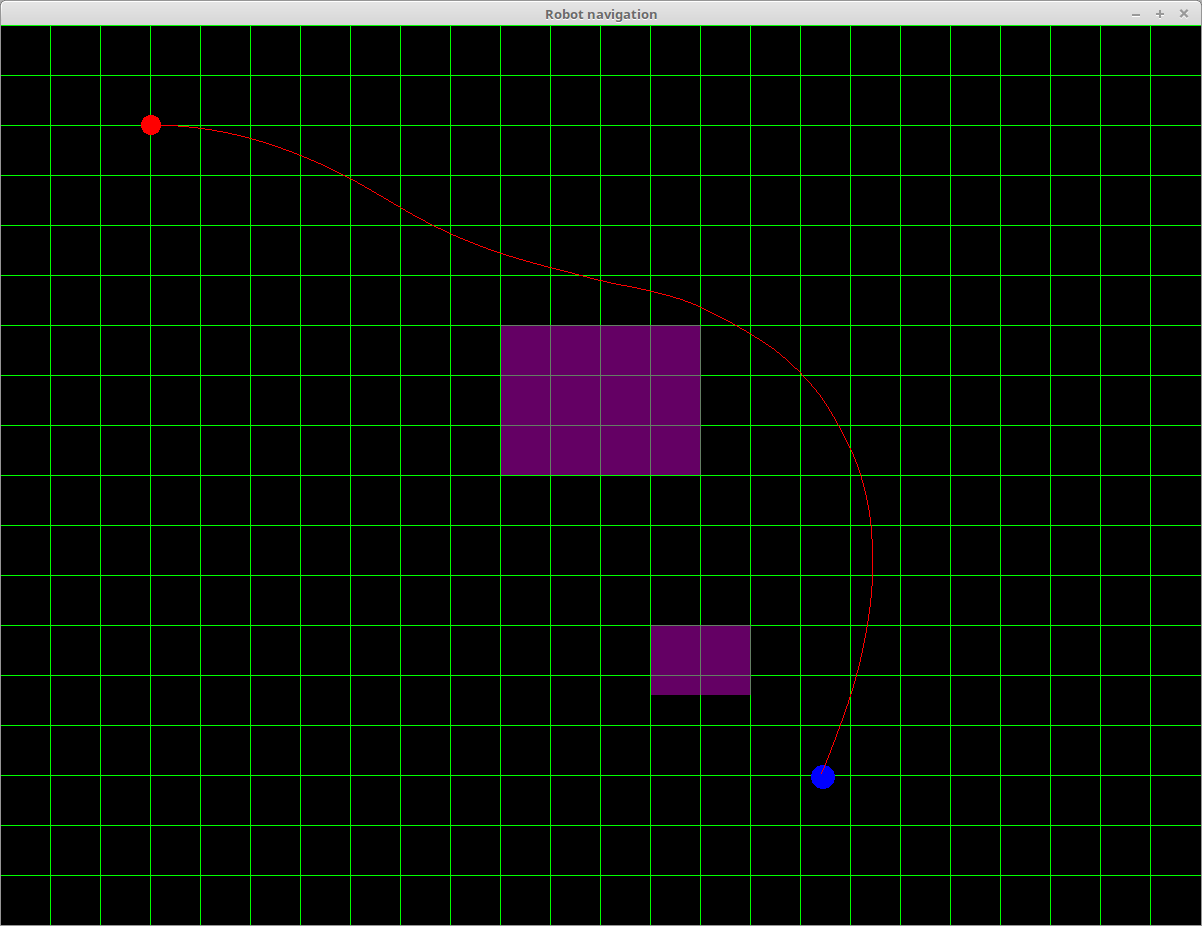
A trajectory with 2 obstacles.
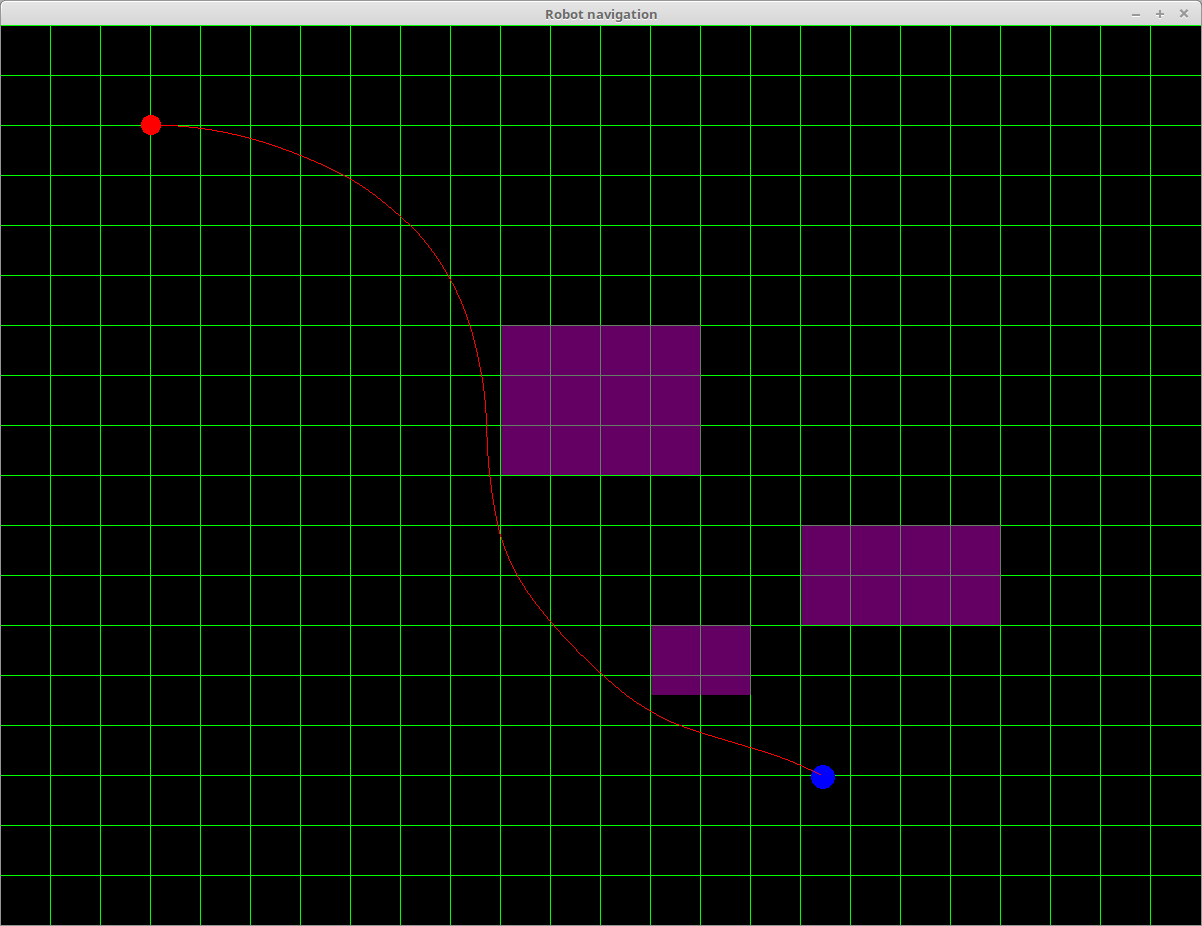
A trajectory with 3 obstacles, the third placed in addition to the prior obstacles to force a path recalculation.
One issue that became clear during implementation was the relatively low speed of the robot motor loop versus the fidelity of the forward model integrator. The robot can update its motors at a frequency of 10Hz, that is its inner loop runs ten times per second. Using a timestep of 0.1s with the forward model integrator resulted in lower accuracy paths. To make the trajectory more accurate, in the examples the forward model was run at a timestep of 0.02s, that is, it ran the same motor command five times over the reduced timestep to get a more accurate next state.
Conclusions
It was anticipated that the high branching factor and necessary discretization for A* might make the approach unworkable — either too many nodes resulting in very long execution time and high memory usage, or that the discretization would make it too inaccurate for use. However the produced inverse model does seem to work to produce smoother and faster movement trajectories within reasonable time frames.
Interestingly, adding obstacles seems to speed up the algorithm rather than slow it down. This is probably because it reduces the search space and the code computing collisions is relatively cheap, even in this early version.
In conclusion, the approach does seem promising and we will continue to experiment with it and prepare it for deployment onto Bertrand.
Further Work
Optimisation. The implementation can be quite slow, taking several seconds to compute a trajectory. However, it was written more for proof-of-concept rather than as a final product. Unravelling inner loops, using static memory models and coding in a lower-level language should make it much faster. In addition, since the robot will operate in largely fixed environments, and travelling a finite set of routes, it is possible that motor plans can be pre-computed and/or cached (for example, if the robot has already calculated a plan to get from one point in a room to the another point on the other side, and finds itself in a different location but closer to the start point of the cached plan than the desired end location, it can navigate faster to the start point of the cached plan and then execute the cached plan).
Forward Model. The forward model is a simple kinematics model of idealised robot trajectory. For deployment it could be quite inaccurate without calibration.
Spatial Model. Currently the spatial model is very rudimentary, using axes-aligned rectangles for obstacles and collision detection. The next step here is probably to implement collision detection for arbitrarily aligned convex hulls, to better represent the obstacles that will be present, and to generate detailed maps of the target environments.
Other Robots. If the state space available to a robot can be formulated as a graph traversable by simulation with the forward model, then graph search algorithms such as A* are the general solution to the inverse model problem. Because of this, it should be possible to use this approach to create inverse models for other robot actions such as reach-and-grasp actions, or even task sub-goaling.