Forward Dynamics Model of a 5 Degree-of-Freedom Robot Arm using DynaMechs
Revision 1.0 2022-09-14
Revision 2.0 2023-10-16
DynaMechs is a dynamics library which performs the physics for chains of rigid bodies. There are many physics engines, but this one in particular looks to have been around for a long time. It's not clear to us whether or not it has been abandoned, although the library is still available to download online. It is interesting to see the source code — it was developed at a time when CPU cycles were precious, and serious efforts were made to make it as optimised as possible. We decided to try to get it working, and our initial goal with it became, to try to use it to develop a forward model for a robot arm. This forward model would be inherently more complex than the kinematics models we normally use, and we would aim to try to use it in predictive control and motor planning, to see what extra demands it would make in such scenarios.
Building DynaMechs
DynaMechs is so venerable it no longer builds with the makefiles in its source distribution. However, this is relatively easy to fix. Here are our modifications to get DynaMechs to build on our target system, Linux x86_64. We aimed to touch the source files as little as possible:-
In make.platform.linux.i686 the CXXFLAGS line becomes:-
CXXFLAGS := -DDM_DOUBLE_PRECISION -pedantic -Wpointer-arith -Wconversion -O2 -s -D_BOOL -Wall -Wuninitialized -c -fPIC -D_POSIX_C_SOURCE=199506L -I/$(OPENGLINCDIR)
The following line in the dm.h, dmGL.h and Gait.hpp files is changed from:
#if defined(WIN32) || (defined(sgi) && defined(_STANDARD_C_PLUS_PLUS)) || (defined(__GNUC__) && (__GNUC__>=2) && (__GNUC_MINOR__>=91))
to:-
#if defined(WIN32) || (defined(sgi) && defined(_STANDARD_C_PLUS_PLUS)) || (defined(__GNUC__) && (((__GNUC__>=2) && (__GNUC_MINOR__>=91)) || (__GNUC__>=3)))
(We did this because g++ was tripped up by the __GNUC_MINOR__ preprocessor definition).
In svd_linpack.cpp change:-
#include <iomanip.h>
to:-
#include <iomanip> #include <iostream> using namespace std;
DynaMechs defines a new type "Float" (not to be confused with "float") to allow the library to be compiled in either single or double precision. We set it to compile with double precision, but in the code their are some instances where "float" seems to be used accidentally. In dm.h we changed this line:-
float norm = sqrt(v[0]*v[0] + v[1]*v[1] + v[2]*v[2]);
to:-
Float norm = sqrt(v[0]*v[0] + v[1]*v[1] + v[2]*v[2]);
There are some instances of this in aquarobot.cpp as well.
Arm Specification
Here we take the convention that the Z-axis is the vertical axis (positive up).
Modified Denavit-Hartenberg Parameters
Each rigid body in the chain is specified in its own coordinate system (describing the origin and axis of movement). DynaMechs uses Modified Denavit-Hartenberg (MDH) parameters to specify how the coordinate system of one link is transformed to become the coordinate system of the next link; thereby connecting the links together in a chain. This requires specifying four parameters: a, alpha, d, and theta. a and d are displacements and alpha and theta are rotation angles. When using rotational joint links, as we do in this project, the a, alpha and d parameters are held fixed and the theta parameter becomes variable, allowing the link to move around that degree of freedom. It can be tricky to work with the MDH parameters to specify a linkage system; fortunately, this page explains it, and has an example of how a Mitsubishi RV-6SDL can be described using the parameters. We decided to use the parameter settings as described on that page, with some slight modifications, and the result is a fictional but hopefully plausible robot arm assembly, using the following MDH parameters:-
| Joint | a (m) | alpha (rad) | d (m) | initial theta (rad) | min theta (rad) | max theta (rad) |
|---|---|---|---|---|---|---|
| R1 | 0.0 | 0.0 | 0.35 | 0.0 | -∞ | ∞ |
| R2 | 0.085 | -π/2 | 0.0 | -1.1 | -1.2 | 0.7 |
| R3 | 0.38 | 0.0 | 0.0 | 0.3 | -π | 0.6 |
| R4 | 0.0 | -π/2 | 0.425 | 0.0 | -π | π |
| R5 | 0.0 | π/2 | 0.0 | 0.0 | -1.1 | 1.1 |
Although the theta parameter is the variable for these joints, an initial theta was specified to pose the robot arm, and maximum and minimum thetas were determined for joint limits. DynaMechs provides a mechanism to set joint limits, and attempts to move a joint past its limits will be opposed by a damped spring equation.
Mass Properties
As the model is a dynamics model, the mass properties of the rigid bodies in the linkage system must be specified. In DynaMechs, these properties are the overall mass of the rigid body, its centre of gravity, and its inertia tensor. To simplify inertia tensor calculation, we decided to model the rigid bodies as axes-aligned cylinders of uniform density (various equations for inertia tensors can be found here). In the cases where rigid body was offset from the origin of its coordinate system, the parallel axis theorem was used to modify the tensor components. The rigid bodies for joints R1 and R2 were modelled as amalgams of two cylinders, to model the large motors that would likely be attached to those joints. The parameters used are described below ('Axis' denotes the principal axis of the cylinder):-
| Joint | Axis | Height (m) | Radius (m) | Mass (kg) | Inertia Tensor (kg m2) | Centre of Gravity (m) |
|---|---|---|---|---|---|---|
| R1 | Z | 0.3 | 0.085 | 3.0 | $$\begin{bmatrix} 0.0279 & 0.0 & 0.0 \\ 0.0 & 0.0279 & 0.0 \\ 0.0 & 0.0 & 0.0108 \end{bmatrix}$$ | $$[ 0.0, 0.0, 0.0 ]$$ |
| Y | 0.14 | 0.05 | 1.5 | $$\begin{bmatrix} 0.0034 & 0.0 & 0.0 \\ 0.0 & 0.0127 & 0.0 \\ 0.0 & 0.0 & 0.0142 \end{bmatrix}$$ | $$[ 0.085, 0.0, 0.0 ]$$ | |
| R2 | X | 0.38 | 0.05 | 1.0 | $$\begin{bmatrix} 0.0013 & 0.0 & 0.0 \\ 0.0 & 0.0488 & 0.0 \\ 0.0 & 0.0 & 0.0488 \end{bmatrix}$$ | $$[ 0.19, 0.0, 0.0 ]$$ | Z | 0.1 | 0.04 | 1.0 | $$\begin{bmatrix} 0.0012 & 0.0 & 0.0 \\ 0.0 & 0.1456 & 0.0 \\ 0.0 & 0.0 & 0.1452 \end{bmatrix}$$ | $$[ 0.38, 0.0, 0.0 ]$$ |
| R3 | Y | 0.425 | 0.04 | 1.0 | $$\begin{bmatrix} 0.0606 & 0.0 & 0.0 \\ 0.0 & 0.0008 & 0.0 \\ 0.0 & 0.0 & 0.0606 \end{bmatrix}$$ | $$[ 0.0, 0.2125, 0.0 ]$$ |
| R4 | Y | 0.1 | 0.02 | 0.3 | $$\begin{bmatrix} 0.00028 & 0.0 & 0.0 \\ 0.0 & 0.00006 & 0.0 \\ 0.0 & 0.0 & 0.00028 \end{bmatrix}$$ | $$[ 0.0, 0.0, 0.0 ]$$ |
| R5 | Y | 0.085 | 0.01 | 0.2 | $$\begin{bmatrix} 0.00049 & 0.0 & 0.0 \\ 0.0 & 0.00001 & 0.0 \\ 0.0 & 0.0 & 0.00049 \end{bmatrix}$$ | $$[ 0.0, 0.0425, 0.0 ]$$ |
Motor Model
DynaMechs includes a DC motor model which can be used to drive the arm joints, converting voltage into torque. The model is quite complete, incorporating parameters for brush drop, armature resistance, friction etc. In these initial experiments we decided to use a simplified set of parameters, and assume the brush drop, rotor inertia and friction are negligable. The resulting motor equations used were:-
$$\displaystyle K_{e} = K_{p}$$
$$\displaystyle V_{s} = K_{e} \times \omega + I_{a} \times R_{a}$$
$$\displaystyle T = K_{p} \times I_{a}$$
Where \(K_{p}\) is the torque constant, \(K_{e}\) is the back EMF constant, \(V_{s}\) is the voltage applied to the motor, \(\omega\) is the angular velocity, \(I_{a}\) is the armature current, \(R_{a}\) is the armature resistance and \(T\) is the output torque.
Ultimately to simplify even further we set \(R_{a}\) to unity, requiring us to specify only \(K_{p}\) for the joint motors, which we did as follows:-
| Motor for joint | \(K_{p}\) |
|---|---|
| R1 | 10.0 |
| R2 | 10.0 |
| R3 | 10.0 |
| R4 | 1.0 |
| R5 | 1.0 |
When and if we come to construct a robot arm of this nature we would of course be able to supply the other parameters from the motor data sheets. Although the motor model is greatly simplified, it does present interesting effects, for example if no source voltage is supplied then the robot joints do not just immediately collapse under gravity as the resultant back EMF produces a torque opposing the motion.
Simulating the Arm
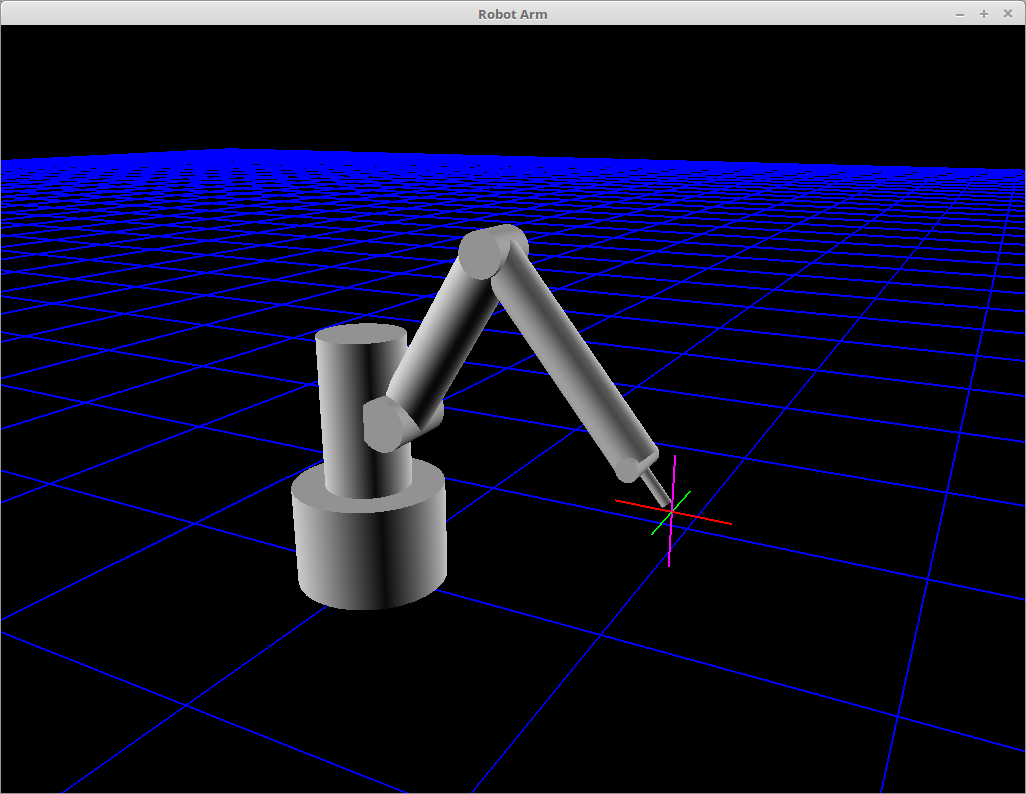
Although the model of the arm is itself mathematical, it is always useful to see what it looks like and how it operates in a simulation. To that end we produced a simulation of the robot in the same format as the other examples provided by DynaMechs, which use the GLUT library to handle display and to process mouse and keyboard input. The OpenGL visualisation was constructed using cylinders matching the MDH parameters and shape properties as described above. The below image is a screenshot from the program.
To prevent the robot arm from collapsing under gravity, simple PD controllers were put on the arm joints to provide motor voltages to keep the joints in their target poses.
Constructing the Forward Model
DynaMechs has several examples of simulated linkage systems in its testdm/ directory. However, to make the forward model, it's not quite enough just to be able to run a simulation loop of a robot; The forward model function has to be constructed so that any robot state and joint forces can be passed in, and the next state (after a specified timestep) be returned. The robot arm state and joint inputs have to be set, the integration performed, and the resultant arm state extracted to be returned to the caller.
State Definition
As the robot arm has five joints each of one degree of freedom, and the dynamics model is second order, the state vector has at least fifteen entries; one each of the position, velocity and acceleration for each of the five joints. We then define three additional states — the (x,y,z) coordinate of an end-effector location (we do not model an end-effector in this report). We do this since it is likely that it is the end-effector location that we ultimately will be wanting to control. DynaMechs provides a function to run the forward kinematics for a linkage system and thereby get the transformation matrix to calculate the end-effector location in the world frame (the location is show as a cross-hair in the image above).
The motors also have internal state information which has to be preserved for a complete representation of the system; specifically, whether the motor is in stiction, and to assist in computing that, the joint velocity at the previous time step. For this robot there are therefore ten extra states, two for each joint, specifying the stiction and the previous velocity. This results in a final state vector which is 28 doubles in size.
The joint input is a vector of five doubles, each specifying a voltage (positive or negative) to apply to one of the five joint motors.
Implementation
At this point, we had to modify the library slightly to extract internal state from DynaMechs. DynaMechs includes a function to return a joint state in terms of its position and velocity, but not its acceleration, which is required for the integration. This is probably because the accelerations are directly computable from the forces in the joints, however it was still much more convenient for us to pull that internal state out of the DynaMechs engine. To do that we added a new method 'AS_getState' to the dmMDHLink.cpp and dmMDHLink.h files.
The following declaration was added to the public section of the 'dmMDHLink' class in dmMDHLink.hpp:-
void AS_getState(Float q[], Float qd[], Float qdd[]) const;
And the body of the method was put in the dmMDHLink.cpp:-
void dmMDHLink::AS_getState(Float q[], Float qd[], Float qdd[]) const
{
qdd[0] = m_qdd;
qd[0] = m_qd;
q[0] = getJointPos();
}
The 'AS_getState' method could then be called to retrieve the position, velocity and acceleration for a joint. Similar simple methods were added in order to retrieve and restore the motor state.
Finally, the implemented code was arranged to create a shared library so that the robot arm forward model could be accessed from other code. The code for this library is below.
Testing
When the forward model is looped with the next state output becoming the current state input, this should result in the same state sequence being generated as when performing a normal simulation of the robot arm, so long as the same motor voltages and timestep are used between the two. To confirm this, we implemented a 'recording' function in the robot simulation, which would store the start state and the voltages applied to the joint motors for a period of time thereafter; the forward model would then be run from the same start state and with the same voltages and timestep applied, and the final states from both modes compared. This proved at least that the forward model could replicate the usual DynaMechs simulation.
We were interested to make the forward model callable from a higher-level language so we could easily perform experiments and log results. We used the FFI::Platypus Perl module to load the library and call the forward model function from Perl. As an experiment, we decided to try to compute the P and I parameters for a PI controller to make the robot arm keep a pose, against gravity. The PI controller would work on the error in the difference from the target pose to calculate voltages to apply to the robot arm's (simulated) motors.
To do this we tried a model-based optimization approach which used the Nelder and Mead Simplex method on an objective function. The Math::Amoeba Perl module provides the Nelder and Mead Simplex, so with a bit of experimentation it was straightforward to put a script together to do this (see here). The objective function is a short simulation of the robot arm over a few seconds, which accumulates the absolute error (deviation) from the target pose. The objective is to minimize this error by selecting candidate parameters. The P parameters are determined first, then the I parameters.
The script executes fairly quickly on our computers, but would likely be prohibitively slow if the arm dynamics themselves were implemented in Perl. The parameters produced were plugged back into the main simulation and do indeed keep the arm stable for the given target pose, however if the target pose is changed significantly the arm does blow up, which is to be expected as the forces on the arm will be very different in different positions. A more comprehensive approach, or at the very least good D parameters, would be needed to control the arm in all situations.
Conclusions and Further Work
For this project we used DynaMechs to build a forward model of a five degree-of-freedom robot arm. We do not have a physical robot arm currently to model, so this robot arm is by necessity somewhat fictional, but hopefully not implausible. The dynamics calculations involved in the model are significantly more involved than with a kinematics model, so we are interested to see how well it can be used in different types of predictive controllers, and for motor planning.
Now that we have our own build of DynaMechs, it is tempting to continue to add to it. DynaMechs provides explicit Euler and some Runge-Kutta integrators. This current model uses explicit Euler, and therefore requires a relatively small timestep to prevent explosions — implementing a Verlet method might provide a good trade-off in terms of stability, speed and accuracy. There is also a contact model in DynaMechs for terrain heightmaps, but not for the rigid bodies themselves, although this should be relatively straightforward to add and potentially allow for the possibility of modelling a gripper or other type of end effector for the arm to manipulate objects.